
Control of Infinite Dimensional Systems
Research Question
Can optimal control techniques be efficiently and effectively applied to infinite dimensional systems?
Summary
Real-world autonomous systems often have dynamics that are best described by infinite dimensional systems. For example, PDE-constrained systems that require aerodynamic modeling (UAV control) or structural deformation modeling (soft robotics). Current frameworks for design and simulation of infinite dimensional systems, such as computational fluid dynamics (CFD) and finite element methods (FEM), are well established. However, they often fall short in the context of control applications due to their heavy computational complexity. This project investigates the use of reduced order models to address this shortcoming, especially for use within the framework of model predictive control.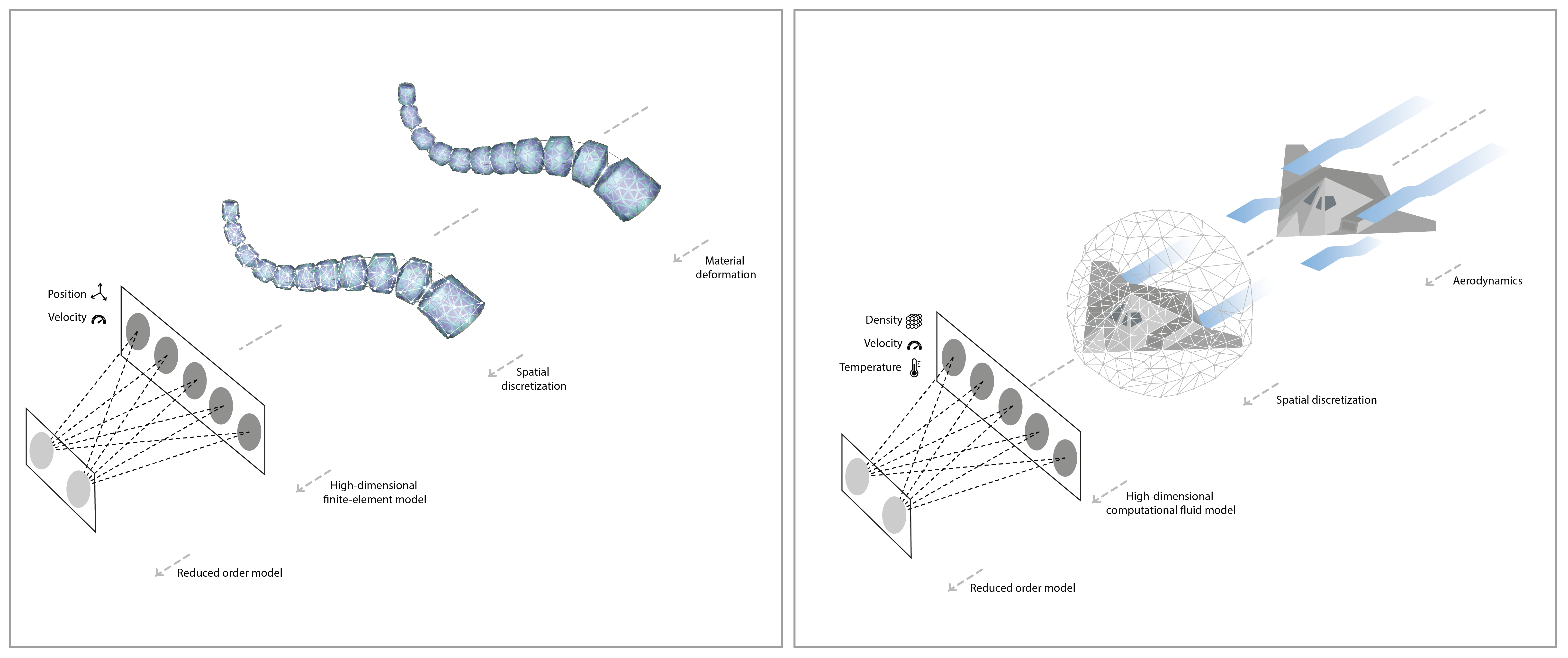

Related Works
-
J. I. Alora, M. Cenedese, E. Schmerling, G. Haller, and M. Pavone, “Practical Deployment of Spectral Submanifold Reduction for Optimal Control of High-Dimensional Systems,” in IFAC World Congress, 2023. (Submitted)
Abstract: Real-time optimal control of high-dimensional, nonlinear systems remains a challenging task due to the computational intractability of their models. While several model-reduction and learning-based approaches for constructing low-dimensional surrogates of the original system have been proposed in the literature, these approaches suffer from fundamental issues which limit their application in real-world scenarios. Namely, they typically lack generalizability to different control tasks, ability to trade dimensionality for accuracy, and ability to preserve the structure of the dynamics. Recently, we proposed to extract low-dimensional dynamics on Spectral Submanifolds (SSMs) to overcome these issues and validated our approach in a highly accurate simulation environment. In this manuscript, we extend our framework to a real-world setting by employing time-delay embeddings to embed SSMs in an observable space of appropriate dimension. This allows us to learn highly accurate, low-dimensional dynamics purely from observational data. We show that these innovations extend Spectral Submanifold Reduction (SSMR) to real-world applications and showcase the effectiveness of SSMR on a soft robotic system.
@inproceedings{AloraCenedeseEtAl2023b, author = {Alora, J.I. and Cenedese, M. and Schmerling, E. and Haller, G. and Pavone, M.}, booktitle = {{IFAC World Congress}}, title = {Practical Deployment of Spectral Submanifold Reduction for Optimal Control of High-Dimensional Systems}, year = {2023}, keywords = {sub}, owner = {jjalora}, timestamp = {2022-11-15}, url = {/wp-content/papercite-data/pdf/Alora.Cenedese.IFAC23.pdf} } -
J. I. Alora, M. Cenedese, E. Schmerling, G. Haller, and M. Pavone, “Data-Driven Spectral Submanifold Reduction for Nonlinear Optimal Control of High-Dimensional Robots,” in Proc. IEEE Conf. on Robotics and Automation, 2023. (Submitted)
Abstract: Modeling and control of high-dimensional, nonlinear robotic systems remains a challenging task. While various model- and learning-based approaches have been proposed to address these challenges, they broadly lack generalizability to different control tasks and rarely preserve the structure of the dynamics. In this work, we propose a new, data-driven approach for extracting low-dimensional models from data using Spectral Submanifold Reduction (SSMR). In contrast to other data-driven methods which fit dynamical models to training trajectories, we identify the dynamics on generic, low-dimensional attractors embedded in the full phase space of the robotic system. This allows us to obtain computationally-tractable models for control which preserve the system’s dominant dynamics and better track trajectories radically different from the training data. We demonstrate the superior performance and generalizability of SSMR in dynamic trajectory tracking tasks vis-a-vis the state of the art.
@inproceedings{AloraCenedeseEtAl2023, author = {Alora, J.I. and Cenedese, M. and Schmerling, E. and Haller, G. and Pavone, M.}, booktitle = {{Proc. IEEE Conf. on Robotics and Automation}}, title = {Data-Driven Spectral Submanifold Reduction for Nonlinear Optimal Control of High-Dimensional Robots}, year = {2023}, keywords = {sub}, owner = {rdyro}, timestamp = {2022-09-21}, url = {https://arxiv.org/abs/2209.05712} } -
F. Mahlknecht, J. I. Alora, S. Jain, E. Schmerling, R. Bonalli, G. Haller, and M. Pavone, “Using Spectral Submanifolds for Nonlinear Periodic Control,” in Proc. IEEE Conf. on Decision and Control, 2022. (Submitted)
Abstract: Very high dimensional nonlinear systems arise in many engineering problems due to semi-discretization of the governing partial differential equations, e.g. through finite element methods. The complexity of these systems present computational challenges for direct application to automatic control. While model reduction has seen ubiquitous applications in control, the use of nonlinear model reduction methods in this setting remains difficult. The problem lies in preserving the structure of the nonlinear dynamics in the reduced order model for high-fidelity control. In this work, we leverage recent advances in Spectral Submanifold (SSM) theory to enable model reduction under well-defined assumptions for the purpose of efficiently synthesizing feedback controllers.
@inproceedings{MahlknechtAloraEtAl2022, author = {Mahlknecht, F. and Alora, J.I. and Jain, S. and Schmerling, E. and Bonalli, R. and Haller, G. and Pavone, M.}, booktitle = {{Proc. IEEE Conf. on Decision and Control}}, title = {Using Spectral Submanifolds for Nonlinear Periodic Control}, year = {2022}, keywords = {sub}, owner = {jjalora}, timestamp = {2022-11-22}, url = {https://arxiv.org/abs/2209.06573} } -
S. Tonkens, J. Lorenzetti, and M. Pavone, “Soft Robot Optimal Control Via Reduced Order Finite Element Models,” in Proc. IEEE Conf. on Robotics and Automation, Xi’an, China, 2021. (Submitted)
Abstract: Finite element methods have been successfully used to develop physics-based models of soft robots that capture the nonlinear dynamic behavior induced by continuous deformation. These high-fidelity models are therefore ideal for designing controllers for complex dynamic tasks such as trajectory optimization and trajectory tracking. However, finite element models are also typically very high-dimensional, which makes real-time control challenging. In this work we propose an approach for finite element model-based control of soft robots that leverages model order reduction techniques to significantly increase computational efficiency. In particular, a constrained optimal control problem is formulated based on a nonlinear reduced order finite element model and is solved via sequential convex programming. This approach is demonstrated through simulation of a cable-driven soft robot for a constrained trajectory tracking task, where a 9768-dimensional finite element model is used for controller design.
@inproceedings{TonkensLorenzettiEtAl2021, author = {Tonkens, S. and Lorenzetti, J. and Pavone, M.}, title = {Soft Robot Optimal Control Via Reduced Order Finite Element Models}, booktitle = {{Proc. IEEE Conf. on Robotics and Automation}}, year = {2021}, note = {Submitted}, address = {Xi'an, China}, month = may, keywords = {sub}, owner = {stonkens}, url = {https://arxiv.org/abs/2011.02092}, timestamp = {2020-11-02} } -
J. Lorenzetti, A. McClellan, C. Farhat, and M. Pavone, “Linear Reduced Order Model Predictive Control,” IEEE Transactions on Automatic Control, 2021. (Submitted)
Abstract: Model predictive controllers leverage system dynamics models to solve constrained optimal control problems. However, computational requirements for real-time control have limited their use to systems with low-dimensional models. Nevertheless many systems naturally produce high-dimensional models, such as those modeled by partial differential equations that when discretized can result in models with thousands to millions of dimensions. In such cases the use of reduced order models (ROMs) can significantly reduce computational requirements, but model approximation error must be considered to guarantee controller performance. In this work a reduced order model predictive control (ROMPC) scheme is proposed to solve robust, output feedback, constrained optimal control problems for high-dimensional linear systems. Computational efficiency is obtained by leveraging ROMs obtained via projection-based techniques, and guarantees on robust constraint satisfaction and stability are provided. Performance of the approach is demonstrated in simulation for several examples, including an aircraft control problem leveraging an inviscid computational fluid dynamics model with dimension 998,930.
@article{LorenzettiMcClellanEtAl2021, author = {Lorenzetti, J. and McClellan, A. and Farhat, C. and Pavone, M.}, title = {Linear Reduced Order Model Predictive Control}, journal = {{IEEE Transactions on Automatic Control}}, year = {2021}, note = {Submitted}, url = {https://arxiv.org/abs/2012.03384}, keywords = {sub}, owner = {jlorenze}, timestamp = {2020-12-04} } -
J. Lorenzetti and M. Pavone, “Error Bounds for Reduced Order Model Predictive Control,” in Proc. IEEE Conf. on Decision and Control, Jeju Island, Republic of Korea, 2020. (Submitted)
Abstract: Model predictive control is a powerful framework for enabling optimal control of constrained systems. However, for systems that are described by high-dimensional state spaces this framework can be too computationally demanding for real-time control. Reduced order model predictive control (ROMPC) frameworks address this issue by leveraging model reduction techniques to compress the state space model used in the online optimal control problem. While this can enable real-time control by decreasing the online computational requirements, these model reductions introduce approximation errors that must be accounted for to guarantee constraint satisfaction and closed-loop stability for the controlled high-dimensional system. In this work we propose an offline methodology for efficiently computing error bounds arising from model reduction, and show how they can be used to guarantee constraint satisfaction in a previously proposed ROMPC framework. This work considers linear, discrete, time-invariant systems that are compressed by Petrov-Galerkin projections, and considers output-feedback settings where the system is also subject to bounded disturbances.
@inproceedings{LorenzettiPavone2020b, author = {Lorenzetti, J. and Pavone, M.}, title = {Error Bounds for Reduced Order Model Predictive Control}, booktitle = {{Proc. IEEE Conf. on Decision and Control}}, year = {2020}, note = {Submitted}, address = {Jeju Island, Republic of Korea}, month = dec, url = {https://arxiv.org/pdf/1911.12349.pdf}, keywords = {sub}, owner = {jlorenze}, timestamp = {2020-02-07} } -
J. Lorenzetti, A. McClellan, C. Farhat, and M. Pavone, “UAV Aircraft Carrier Landing Using CFD-Based Model Predictive Control,” in AIAA Scitech Forum, Orlando, Florida, 2020.
Abstract: The control problem associated with autonomous aircraft carrier landings for UAVs is challenging due to requirements on safety, high-performance operation, and uncertain and highly dynamic environments. This work proposes a control scheme for such problems that enables safe operation of the UAV at the limits of its performance by utilizing a model predictive control (MPC) approach. While real-time computation requirements typically limit the fidelity of the models used in optimization-based control, in this work it is demonstrated that high-fidelity computational fluid dynamics (CFD) models can be used within an MPC framework via the construction of a projection-based reduced order model (ROM). An application of a CFD-based MPC scheme to the glideslope tracking problem is then developed to demonstrate the effectiveness of the proposed approach.
@inproceedings{LorenzettiMcClellanEtAl2020, author = {Lorenzetti, J. and McClellan, A. and Farhat, C. and Pavone, M.}, title = {{UAV} Aircraft Carrier Landing Using {CFD}-Based Model Predictive Control}, booktitle = {{AIAA Scitech Forum}}, year = {2020}, address = {Orlando, Florida}, month = jan, url = {/wp-content/papercite-data/pdf/Lorenzetti.McClellan.Farhat.Pavone.AIAA20.pdf}, owner = {jlorenze}, timestamp = {2019-12-02} } -
A. McClellan, J. Lorenzetti, M. Pavone, and C. Farhat, “Projection-based Model Order Reduction for Flight Dynamics and Model Predictive Control,” in AIAA Scitech Forum, Orlando, Florida, 2020.
Abstract: A model predictive control algorithm seeks to produce a control law that optimizes the future behavior of a deployed system over a finite time horizon, by leveraging a real-time computational model of this system. For applications involving fluid-structure interaction (FSI), this leveraging is challenging because it implies the design of an accurate and yet real-time computational model for the prediction of the time-dependent flow-induced forces and moments acting on the system. The projection-based reduction of CFD-based computational models for FSI provides one approach for addressing this issue. In this context, linear model reduction is adequate as the controller can be expected to maintain the system of interest within small perturbations around a pre-designed optimal trajectory. For the automated landing of an aircraft application considered in this paper, this requires the construction of a CFD-based projection-based reduced-order model that is linearized around a time-dependent trajectory rather than a mere steady-state equilibrium position. To this end, a computational approach for the projection-based model order reduction of linearized CFD-based computational models for FSI is presented, with the goal of application to downstream control tasks such as automated aircraft landing. The approach addresses the issues of linearization around a trajectory and construction of stable reduced-order models to achieve real-time computation, while maintaining model accuracy, and thereby enabling model predictive control. It is verified using a simple model predictive control algorithm.
@inproceedings{McClellanLorenzettiEtAl2020, author = {McClellan, A. and Lorenzetti, J. and Pavone, M. and Farhat, C.}, title = {Projection-based Model Order Reduction for Flight Dynamics and Model Predictive Control}, booktitle = {{AIAA Scitech Forum}}, year = {2020}, address = {Orlando, Florida}, month = jan, url = {https://arc.aiaa.org/doi/abs/10.2514/6.2020-1190}, owner = {jlorenze}, timestamp = {2019-12-02} } -
J. Lorenzetti, B. Landry, S. Singh, and M. Pavone, “Reduced Order Model Predictive Control For Setpoint Tracking,” in European Control Conference, Naples, Italy, 2019.
Abstract: Despite the success of model predictive control (MPC), its application to high-dimensional systems, such as flexible structures and coupled fluid/rigid-body systems, remains a largely open challenge due to excessive computational complexity. A promising solution approach is to leverage reduced order models for designing the model predictive controller. In this paper we present a reduced order MPC scheme that enables setpoint tracking while robustly guaranteeing constraint satisfaction for linear, discrete, time-invariant systems. Setpoint tracking is enabled by designing the MPC cost function to account for the steady-state error between the full and reduced order models. Robust constraint satisfaction is accomplished by solving (offline) a set of linear programs to provide bounds on the errors due to bounded disturbances, state estimation, and model approximation. The approach is validated on a synthetic system as well as a high-dimensional linear model of a flexible rod, obtained using finite element methods.
@inproceedings{LorenzettiLandryEtAl2019, author = {Lorenzetti, J. and Landry, B. and Singh, S. and Pavone, M.}, title = {Reduced Order Model Predictive Control For Setpoint Tracking}, booktitle = {{European Control Conference}}, year = {2019}, address = {Naples, Italy}, month = jun, url = {https://arxiv.org/pdf/1811.06590.pdf}, owner = {jlorenze}, timestamp = {2019-04-26} }